공부전 나의 상태
Python : 공부한적은 있지만 아주 아주 초급 문법만 사용함...TensorFlow : 공부한적은 있지만 아주 초급 문법도 사용할줄 모르는 상태
PyTorch : 쌩판 모름
공부 대상
https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html이번에는 autograd 라는 주제입니다.
Autograd: automatic differentiation
PyTorch에서 자동 미분값 계산은 autograd 패키지가 해줍니다. 간단한 예제를 살펴보면서 공부를 하면 좀 더 이해하기 쉽습니다.
미분값이 왜 필요할까요?? Feedback을 다시 입력을 넣는 미분 제어 방식을 Neural Network 방식을 사용하고 있는데 이것을 일반적으로 Back propagation 이라고 합니다.
Tensor
torch.Tensor에서 .requires_grad 속성을 True로 설정하면 연산을 추적할 준비가 끝납니다. 그리고 계산을 마쳤을때 .backward() 함수를 호출하면 기울기를 자동으로 계산해줍니다. 계산된 값은 .grad 속성에 누적됩니다.
tensor 트랙을 중지하려면 .detach()를 호출하면 됩니다.
또한 트랙킹 history를 막기위해서 with torch.no_grad(): 코드 블럭안에 기록할 수 있습니다. (이 부분은 아래 예에 나옵니다.)
각각의 텐서들을은 텐서에 의해 생성된 function을 가진 .grad_fn 속성을 가지고 있습니다. (단, 사용자에 의해 생성된 텐서는 제외, 사용자에 의해 생성된 grad_fn 이 None 입니다. )
미분계산을 위해서는 텐서의 .backward() 를 호출하면 됩니다. 만약 tensor가 스칼라(즉, 하나의 엘리먼트인 경우)이면, backward()의 인자를 기록할 필요는 없습니다. 그러나 여러개의 값들을 가진경우, 일치하는 형태의 텐서 인자를 열거해야 합니다.
위 내용은 영문 튜토리얼을 번역한 형태라서 자세한 내용은 예제 설명으로 차근차근 살펴볼 예정입니다.
pytorch 사용하기 위한 기본 코드
import torch
(autograd를 위해서) requires_grad=True로 해서 텐서를 생성합니다. 2*2 크기의 텐서가 생성되고 그안에는 1,1,1,1 의 값을 가지게 됩니다.
x = torch.ones(2, 2, requires_grad=True) print(x)
아직까지는 아무런 동작을 안했기 때문에 2*2의 텐서에 1 값이 나옵니다.
Out:
tensor([[ 1., 1.],
[ 1., 1.]])
y = x + 2 print(y)
출력을 해보면 텐서 y는 3이 되었습니다.
Out:
tensor([[ 3., 3.],
[ 3., 3.]])
print(y.grad_fn)
grad_fn에 어떤 값이 들어있는것을 알 수 있습니다.
Out:
<AddBackward0 object at 0x7f12da7f6a20>
z = y * y * 3 out = z.mean() print(z, out)
(1+2)*(1+2)*3=27이 될것 입니다.
그리고 z.mean()은 텐서의 평균값을 나타내므로 27*4/4 = 27이 됩니다.
Out:
tensor([[ 27., 27.],
[ 27., 27.]]) tensor(27.)
a = torch.randn(2, 2) a = ((a * 3) / (a - 1)) print(a.requires_grad) a.requires_grad_(True) print(a.requires_grad) b = (a * a).sum() print(b.grad_fn)
Out:
False
True
<SumBackward0 object at 0x7f12da7f62b0>
Gradients
위에서 out = z.mean() 이런식으로 했습니다. 이것은 하나의 원소를 같는 형태입니다. 그래서 out.backward()와 out.backward(torch.tensor(1)) 와 동일합니다.
앞에서 다음과 같은 언급을 하였습니다.
"만약 tensor가 스칼라(즉, 하나의 엘리먼트인 경우)이면, backward()의 인자를 기록할 필요는 없습니다. 그러나 여러개의 값들을 가진경우, 일치하는 형태의 텐서 인자를 열거해야 합니다."
아래 동작은 backpropagation을 수행합니다. 이것은 자동 미분값을 생성합니다.
out.backward()
이것은 자동 미분값을 생성합니다.
d(out)/dx 값을 출력하려면 x.grad 값을 출력해보면 됩니다.
print(x.grad)
Out:
tensor([[ 4.5000, 4.5000],
[ 4.5000, 4.5000]])
사실 봐도 어려워 보이는데 이것을 풀어보도록 하겠습니다.
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
out을 x에 관한 식으로 써보면, out = ((x+2)*(x+2)*3).mean() 평균값이므로 mean()은 1/4이 됩니다.
미분을 계산해보면 d(out)/d(x) = d((3x^2+12x+12)/4)/d(x) = (3*2/4x+12/4) = (3/2x+3) 여기에서 x는 1이므로 4.5가 됩니다.
참고 미분 공식)
(1) (c는 상수)이면
(2) (n은 실수)이면
x = torch.randn(3, requires_grad=True) y = x * 2 while y.data.norm() < 1000: y = y * 2 print(y)
Out:
tensor([ 640.7057, 792.3956, -1404.8168])
https://pytorch.org/docs/stable/torch.html#torch.norm
https://ko.wikipedia.org/wiki/%EB%85%B8%EB%A6%84_%EA%B3%B5%EA%B0%84
원소들에 일종의 ‘길이’ 또는 ‘크기’가 부여된 벡터 공간이다.
위 예제 코드에서 y.data.norm() 를 부여한건 데이터의 크기 정보를 얻어오기 위함이고 그것이 y=y*2가 몇번 돌았는지 모를 정도로 돌게되면 다음의 수식으로 grad값을 자동으로 얻어 올 수 있음을 보여주는 예제이다.
gradients = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) y.backward(gradients) print(x.grad)
Out:
tensor([ 102.4000, 1024.0000, 0.1024])
"트랙킹 history를 막기위해서 with torch.no_grad(): 코드 블럭안에 기록할 수 있습니다. "
print(x.requires_grad) print((x ** 2).requires_grad) with torch.no_grad(): print((x ** 2).requires_grad)
Out:
True
True
False
예제코드
import torch ############################################################### # Create a tensor and set requires_grad=True to track computation with it x = torch.ones(2, 2, requires_grad=True) print(x) ############################################################### # Do an operation of tensor: y = x + 2 print(y) ############################################################### # ``y`` was created as a result of an operation, so it has a ``grad_fn``. print(y.grad_fn) ############################################################### # Do more operations on y z = y * y * 3 out = z.mean() print(z, out) ################################################################ # ``.requires_grad_( ... )`` changes an existing Tensor's ``requires_grad`` # flag in-place. The input flag defaults to ``True`` if not given. a = torch.randn(2, 2) a = ((a * 3) / (a - 1)) print(a.requires_grad) a.requires_grad_(True) print(a.requires_grad) b = (a * a).sum() print(b.grad_fn) ############################################################### # Gradients # --------- # Let's backprop now # Because ``out`` contains a single scalar, ``out.backward()`` is # equivalent to ``out.backward(torch.tensor(1))``. out.backward() ############################################################### # print gradients d(out)/dx # print(x.grad) ############################################################### # You should have got a matrix of ``4.5``. Let’s call the ``out`` # *Tensor* “:math:`o`”. # We have that :math:`o = \frac{1}{4}\sum_i z_i`, # :math:`z_i = 3(x_i+2)^2` and :math:`z_i\bigr\rvert_{x_i=1} = 27`. # Therefore, # :math:`\frac{\partial o}{\partial x_i} = \frac{3}{2}(x_i+2)`, hence # :math:`\frac{\partial o}{\partial x_i}\bigr\rvert_{x_i=1} = \frac{9}{2} = 4.5`. ############################################################### # You can do many crazy things with autograd! x = torch.randn(3, requires_grad=True) y = x * 2 while y.data.norm() < 1000: y = y * 2 print(y) ############################################################### # gradients = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) y.backward(gradients) print(x.grad) ############################################################### # You can also stop autograd from tracking history on Tensors # with ``.requires_grad``=True by wrapping the code block in # ``with torch.no_grad():`` print(x.requires_grad) print((x ** 2).requires_grad) with torch.no_grad(): print((x ** 2).requires_grad) ############################################################### # **Read Later:** # # Documentation of ``autograd`` and ``Function`` is at # http://pytorch.org/docs/autograd
(base) E:\pytorch>python autograd_tutorial.py
tensor([[ 1., 1.],
[ 1., 1.]])
tensor([[ 3., 3.],
[ 3., 3.]])
<AddBackward0 object at 0x000001E8378EA630>
tensor([[ 27., 27.],
[ 27., 27.]]) tensor(27.)
False
True
<SumBackward0 object at 0x000001E8378EA5C0>
tensor([[ 4.5000, 4.5000],
[ 4.5000, 4.5000]])
tensor([-861.2302, 328.4919, 653.2436])
tensor([ 51.2000, 512.0000, 0.0512])
True
True
False
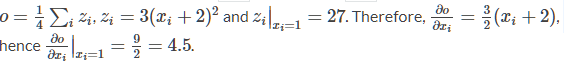
댓글 없음:
댓글 쓰기